[ad_1]
Investors across the globe use the Sharpe Ratio, among other risk-adjusted metrics, to compare the performance of mutual fund and hedge fund managers as well as asset classes and individual securities. The Sharpe Ratio attempts to describe the excess return relative to the risk of the strategy or investment — that is, return minus risk-free rate divided by volatility — and is among the primary gauges of fund manager performance.
But hidden within the Sharpe Ratio is the assumption that volatility — the denominator of the equation — captures “risk” in its entirety. Of course, if volatility fails to entirely reflect the investment’s risk profile, then the Sharpe Ratio and similar risk-adjusted measures may be flawed and unreliable.
What are the implications of such a conclusion? A common one is that the distribution of returns must be normal, or Gaussian. If there is significant skewness in the returns of the security, strategy, or asset class, then the Sharpe Ratio may not accurately describe “risk-adjusted returns.”
To test the metric’s effectiveness, we constructed monthly return distributions for 15 global stock market indices to determine if any had such exacerbated skewness as to call into question the measure’s applicability. The distribution of returns went as far back as 1970 and were calculated on both a monthly and annual basis. The monthly return distributions are presented blow. Annual return results were qualitatively similar across the various indices studied.
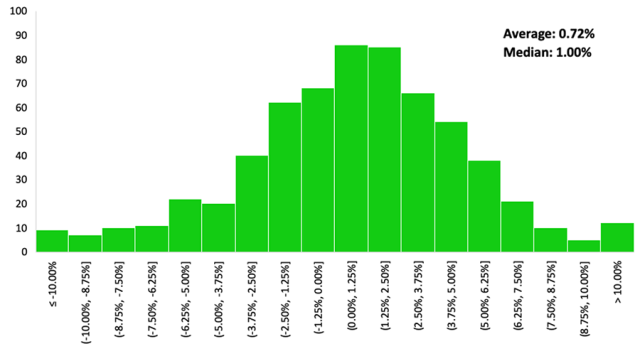
We ranked all 15 indices by their skewness. The S&P 500 came in close to the middle of the pack on this measure, with an average return of 0.72% and a median return of 1% per month. So, the S&P distribution skews just a bit to the left.
S&P 500 Monthly Return Distributions, Since 1970
The complete list of indices ranked by their skewness is presented in the chart below. Ten of the 15 indices exhibit left skewness, or crash risk: They are more prone to pronounced nose-dives than they are to steep upward climbs. The least skewed distributions were those of France’s CAC 40 and the Heng Seng, in Hong Kong, SAR.
Monthly Returns by Global Index
| Index | Mean | Median | Min. | Max. | STD | Skewness |
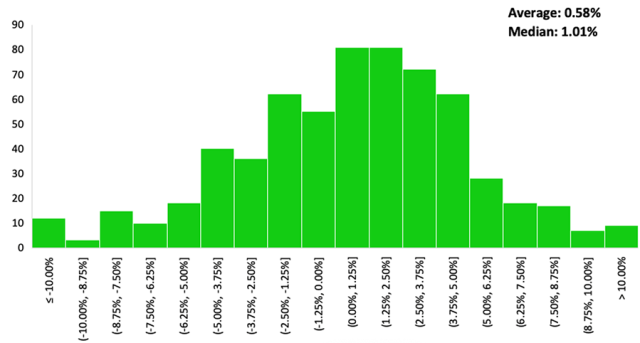
| ASX 200 | 0.58% | 1.01% | -42.3% | 22.4% | 0.048 | -1.3 |
| TSX | 0.60% | 0.88% | -22.6% | 16% | 0.044 | -0.77 |
| FTSE | 0.53% | 0.91% | -27.6% | 13.7% | 0.045 | -0.73 |
| Russell 2000 | 0.84% | 1.60% | -21.9% | 18.3% | 0.055 | -0.55 |
| S&P 500 | 0.72% | 1.00% | -21.8% | 16.3% | 0.044 | -0.45 |
| DAX | 0.67% | 0.74% | -25.4% | 21.4% | 0.056 | -0.39 |
| Nikkei | 0.54% | 0.91% | -23.8% | 20.1% | 0.055 | -0.37 |
| MXX | 1.23% | 1.16% | -29.5% | 20.4% | 0.066 | -0.34 |
| MOEX | 1.29% | 1.63% | -30% | 33% | 0.079 | -0.29 |
| CAC 40 | 0.64% | 0.98% | -22.3% | 24.5% | 0.056 | -0.11 |
| Hang Seng | 1.17% | 1.23% | -44.1% | 67.3% | 0.090 | 0.33 |
| NSE | 1.50% | 1.05% | -24% | 42% | 0.076 | 0.53 |
| KRX | 0.90% | 0.49% | -27.3% | 50.7% | 0.074 | 0.80 |
| BVSP | 5.63% | 1.94% | -58.8% | 128.6% | 0.184 | 2.51 |
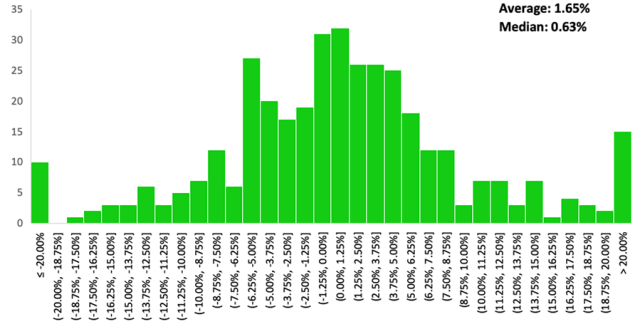
| SSE | 1.65% | 0.63% | -31.2% | 177.2% | 0.151 | 6.26 |
The Shanghai Composite has exhibited the greatest degree of right skewness over time, tending to crash up more than down, and otherwise generating average returns of 1.65% per month and median returns of 0.63% per month.
Shanghai Composite (SSE) Monthly Return Distribution, Since 1990
On the opposite end of the spectrum is the Australian ASX. The ASX has the most left skewness of all the indices, with an average monthly return of 0.58% and median monthly return of 1.01% since 1970.
Australian Stock Exchange (ASX) Monthly Return Distributions, Since 1970
In the end, the BSVA in Brazil, the Shanghai Composite in China, and, to a lesser extent the ASX in Australia just have too much skewness in their returns to validate the Sharpe Ratio as an appropriate measure for their risk-adjusted performance. As a consequence, metrics that account for skewness in returns may be better gauges in these markets.
Of the other indices, seven had fairly symmetrical distributions and five had moderately skewed ones. All told, this suggests that the Sharpe Ratio still has value as a performance metric and that it may not be as obsolete or ineffective as its critics contend.
If you liked this post, don’t forget to subscribe to the Enterprising Investor.
All posts are the opinion of the author. As such, they should not be construed as investment advice, nor do the opinions expressed necessarily reflect the views of CFA Institute or the author’s employer.
Image credit: ©Getty Images/NPHOTOS
Professional Learning for CFA Institute Members
CFA Institute members are empowered to self-determine and self-report professional learning (PL) credits earned, including content on Enterprising Investor. Members can record credits easily using their online PL tracker.
[ad_2]
Image and article originally from blogs.cfainstitute.org. Read the original article here.

